4.1 簡單線性迴歸
線性回歸模型是Yi=β0+β1Xi+ui
STR <- c(15, 17, 19, 20, 22, 23.5, 25)
TestScore <- c(680, 640, 670, 660, 630, 660, 635)plot(TestScore ~ STR,ylab=”Test Score”,pch=20)
abline(a = 713, b = -3)

4.2 估計線性迴歸模型的係數
plot(score ~ STR,data = CASchools,main = “Scatterplot of Test Score and STR”,xlab = “STR (X)”,ylab = “Test Score (Y)”)

觀察值在師生比和考試成績的散佈圖。我們看到這些點強烈地分散,而且這些變數呈負相關。也就是說,我們預期在較大的班級中觀察到較低的分數。
linear_model <- lm(score ~ STR, data = CASchools)
Coefficients:
(Intercept) STR
698.93 -2.28
plot(score ~ STR,data = CASchools,main = “Scatterplot of Test Score and STR”,xlab = “STR (X)”,ylab = “Test Score (Y)”,xlim = c(10, 30),ylim = c(600, 720))
abline(linear_model)

4.3 擬合度量
summary(linear_model)
lm(formula = score ~ STR, data = CASchools)
Residuals:
Min 1Q Median 3Q Max
-47.727 -14.251 0.483 12.822 48.540
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 698.9329 9.4675 73.825 < 2e-16 ***
STR -2.2798 0.4798 -4.751 2.78e-06 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Residual standard error: 18.58 on 418 degrees of freedom
Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897
F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06
R^2:解釋變數 解釋了依變數 的變異數的
殘差標準誤差稱為 。
4.4 最小平方假設
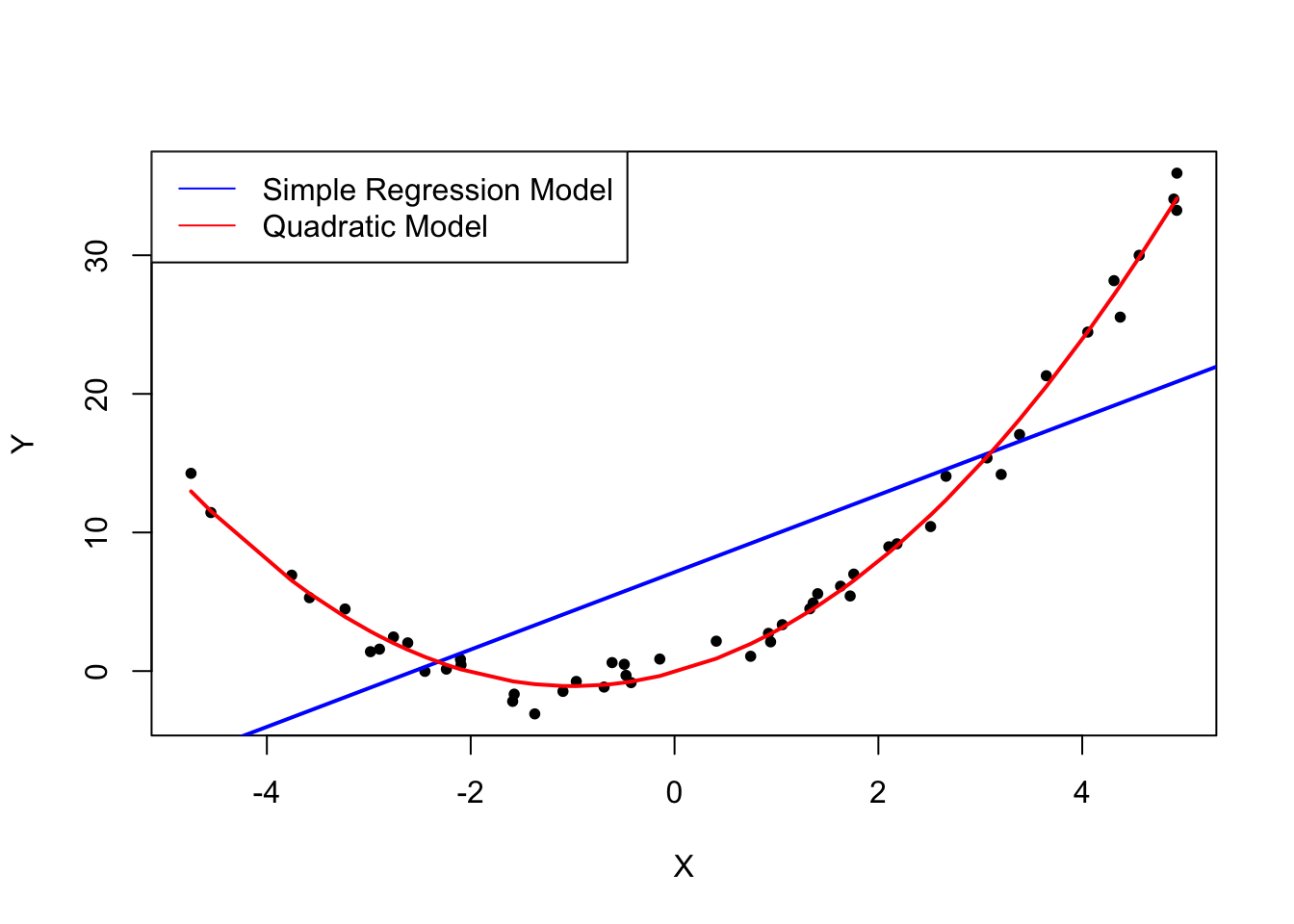
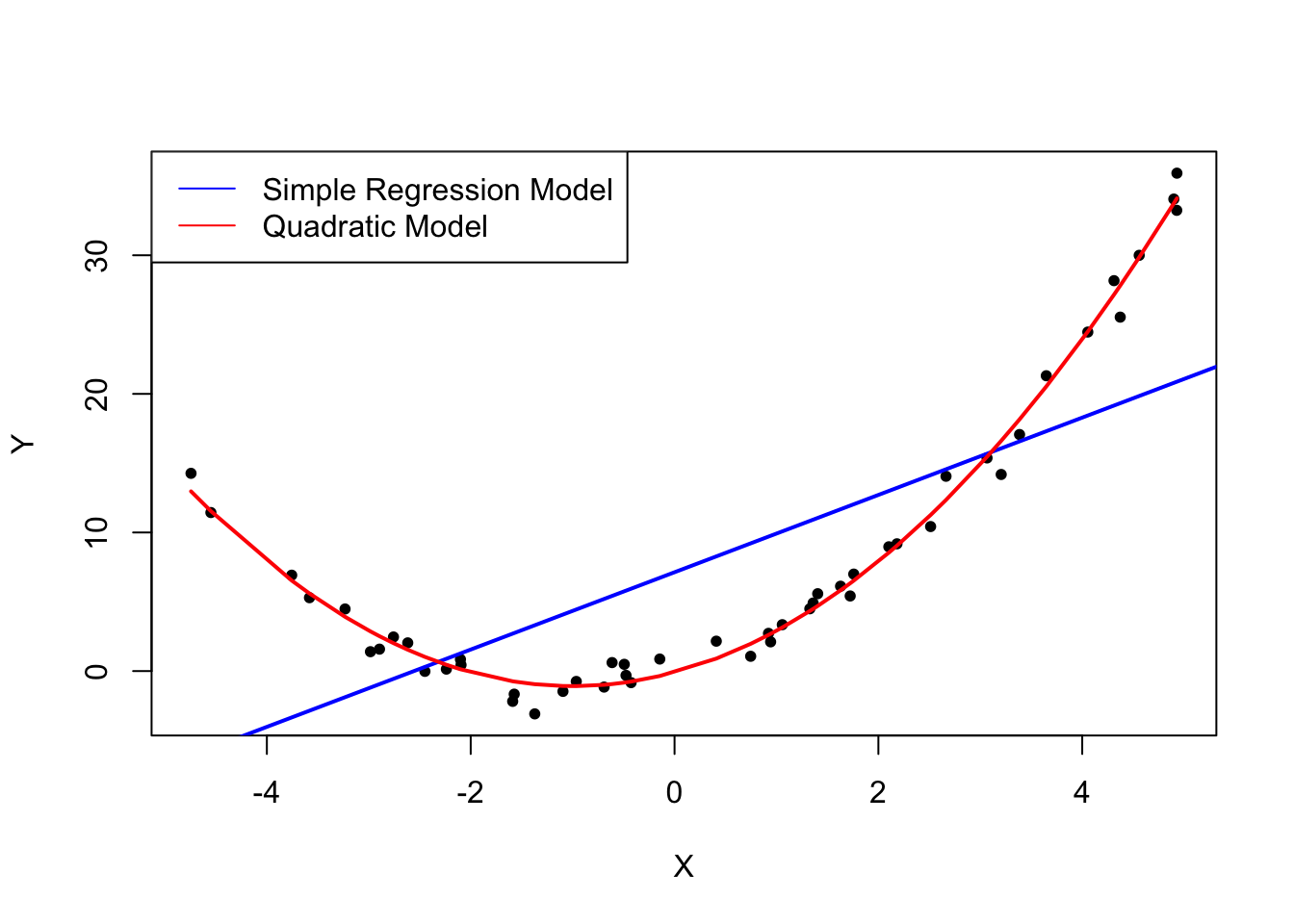
假設 1:誤差項的條件平均值為零
set.seed(321)
# simulate the data
X <- runif(50, min = -5, max = 5)
u <- rnorm(50, sd = 1)# the true relation
Y <- X^2 + 2 * X + u# estimate a simple regression model
mod_simple <- lm(Y ~ X)# estimate a quadratic regression model
mod_quadratic <- lm( Y ~ X + I(X^2))# predict using a quadratic model
prediction <- predict(mod_quadratic, data.frame(X = sort(X)))# plot the results
plot( Y ~ X, col = “black”, pch = 20, xlab = “X”, ylab = “Y”)
abline( mod_simple, col = “blue”,lwd=2)
#red line = incorrect linear regression (this violates the first OLS assumption)
lines( sort(X), prediction,col=”red”,lwd=2)
legend(“topleft”,legend = c(“Simple Regression Model”,”Quadratic Model”),cex = 1,lty = 1,col = c(“blue”,”red”))
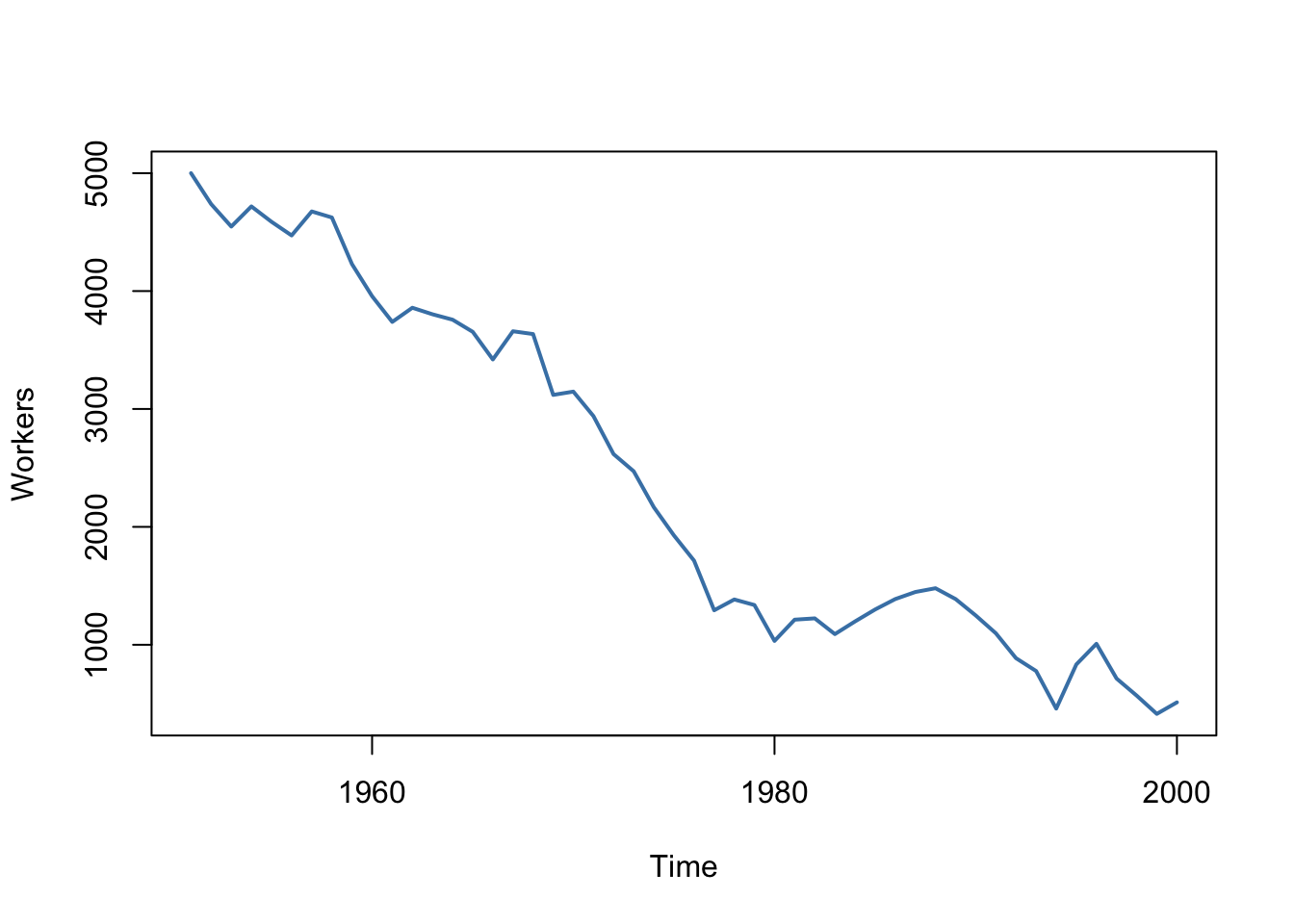
假設 2:獨立同分布資料
這個例子中,對員工數量的觀察不可能是獨立的:今天的就業水平與明天的就業水平相關。違反 i.i.d. 假設。
set.seed(123)
# generate a date vector
Date <- seq(as.Date(“1951/1/1”), as.Date(“2000/1/1”), “years”)# initialize the employment vector
X <- c(5000, rep(NA, length(Date)-1))# generate time series observations with random influences
for (t in 2:length(Date)) {
X[t] <- -50 + 0.98 * X[t-1] + rnorm(n = 1, sd = 200)
}#plot the results
plot(x = Date,y = X,type = “l”,col = “steelblue”,ylab = “Workers”,xlab = “Time”,lwd=2)
假設 3:極端離群值不太可能發生
極端觀察值在未知迴歸係數的估計中會受到很大的權重。因此,異常值可能導致迴歸係數的估計值嚴重失真。
(紅線:無離群值;藍線:加入離群值)
X <- sort(runif(10, min = 30, max = 70))
Y <- rnorm(10 , mean = 200, sd = 50)
Y[9] <- 2000# fit model with outlier
fit <- lm(Y ~ X)# fit model without outlier
fitWithoutOutlier <- lm(Y[-9] ~ X[-9])# plot the results
plot(Y ~ X,pch=20)
abline(fit,lwd=2,col=”blue”)
abline(fitWithoutOutlier, col = “red”,lwd=2)
legend(“topleft”,legend = c(“Model with Outlier”,”Model without Outlier”),cex = 1,lty = 1,col = c(“blue”,”red”))
4.5 OLS 估計量的抽樣分配
估計量的分佈可以很好地近似於關鍵概念 4.4 中所述的各自理論常態分佈。
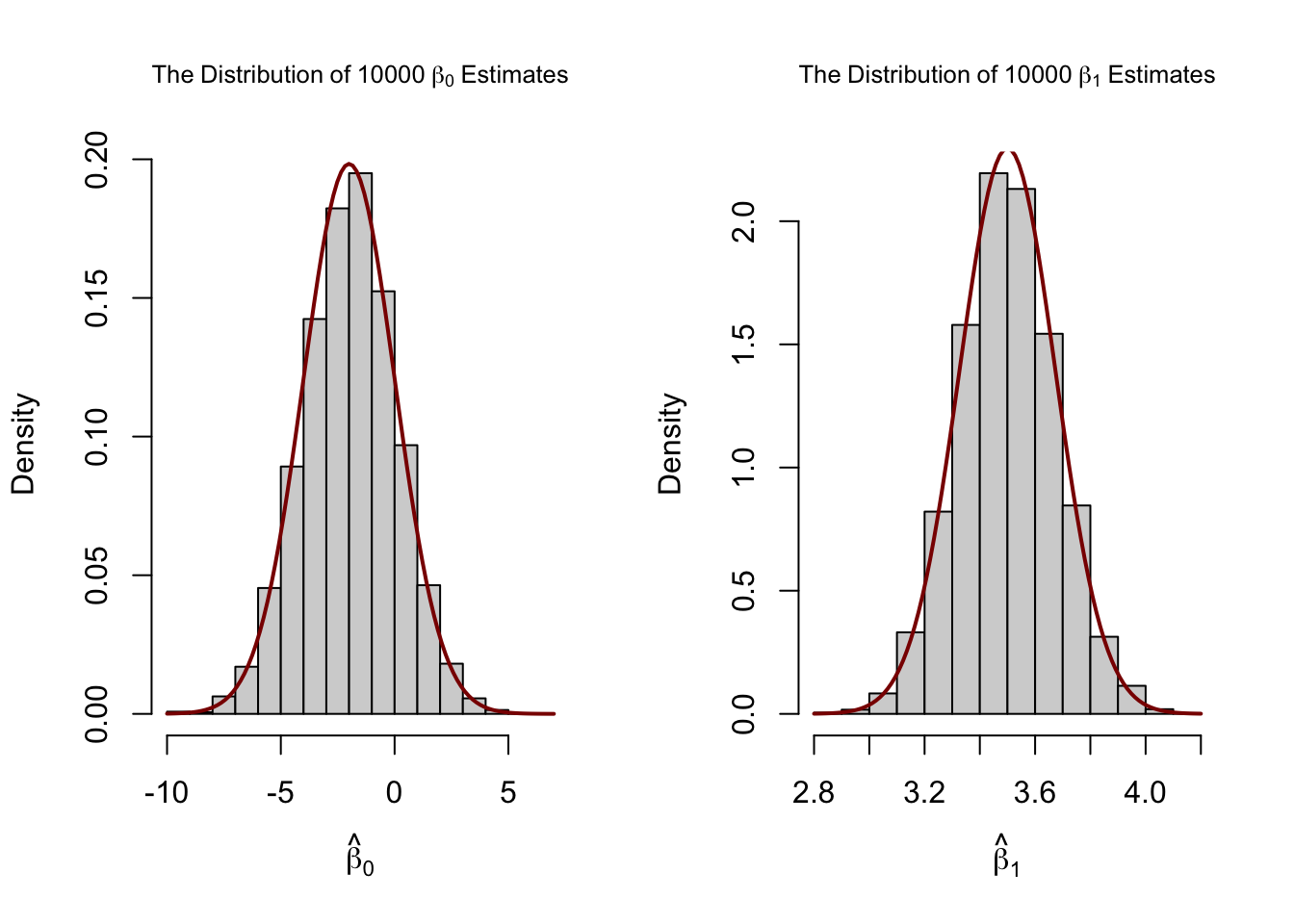
我們發現,隨著 增加, 的分佈集中在其平均值附近,即其變異數減少。
增加樣本量,觀察到接近 真實值的估計值的可能性會增加。
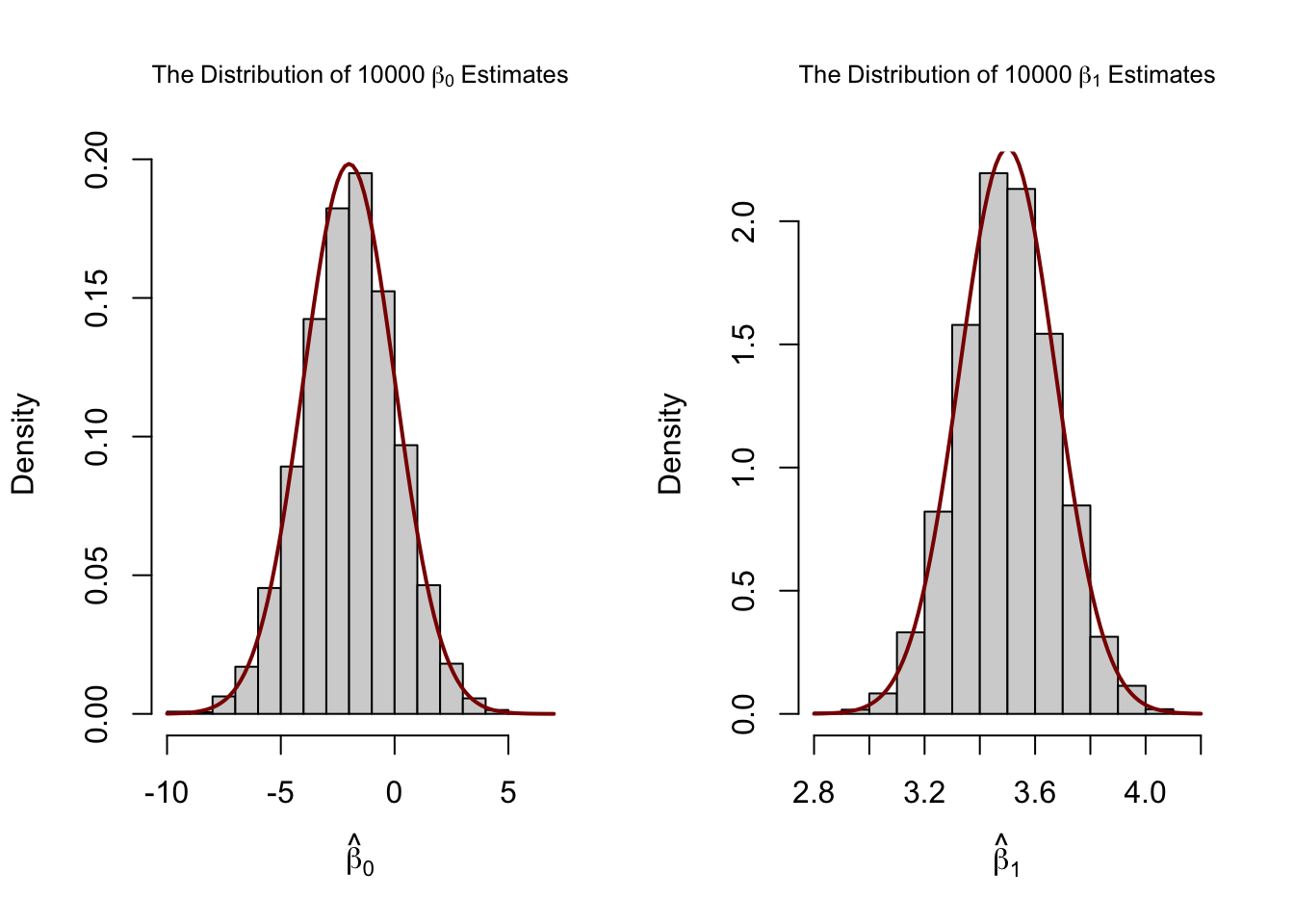
很明顯地,接近樣本平均值的觀察值,其變異性小於那些距離較遠的觀察值。
即使用變異性大於藍色觀察值的觀察值集,將會產生一條更精確的線。
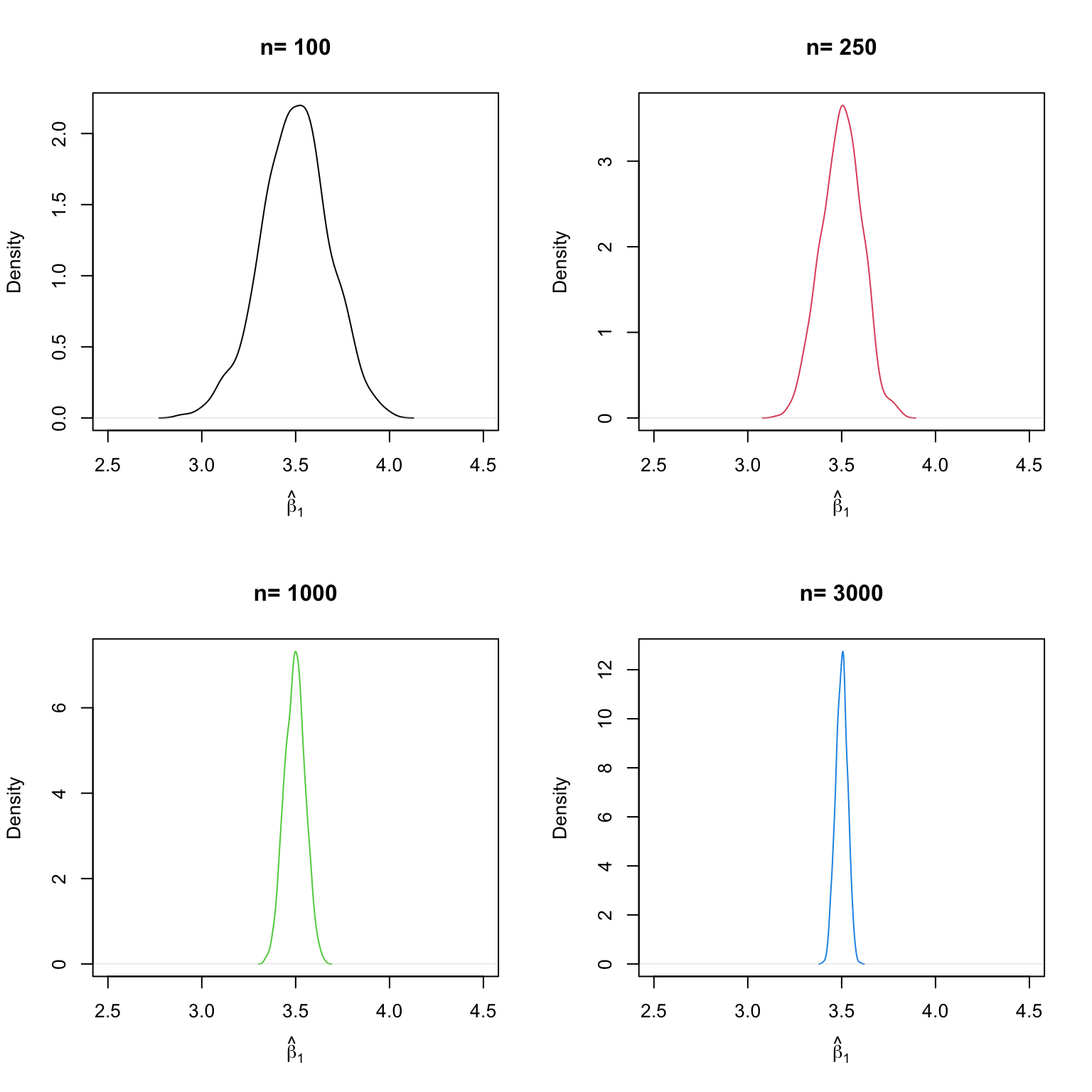
中的變異數越大,可供估計精確度受益的資訊就越多。