計量經濟學作業 U5 簡單線性回歸檢定、信賴區間

5.1 關於斜率係數的雙邊假設檢定

$H_0:{\beta }_1={\beta }_{1,0}$

$H_1:{\beta }_1\ne {\beta }_{1,0}$

data(CASchools)

CASchools$STR <- CASchools$students/CASchools$teachers

CASchools$score <- (CASchools$read + CASchools$math)/2

linear_model <- lm(score ~ STR, data = CASchools)

summary(linear_model)$coefficients

Estimate          Std. Error        t value                  Pr(>|t|)
(Intercept)          698.932949     9.4674911       73.824516           6.569846e-242
STR                     -2.279808        0.4798255       -4.751327          2.783308e-06

可由summary得知， $p\text{-value}=\mathrm{2.78\; *}{10}^{-6}<0.05$ 。

我們得出係數與零顯著不同的結論。換句話說，我們在 $5\%$ 水準下，拒絕課堂規模對學生考試成績沒有影響的假設。

在此t分配的自由度為DF=n−k−1   (=420-1-1 )

n=個數，k=回歸變數(本題為STR)

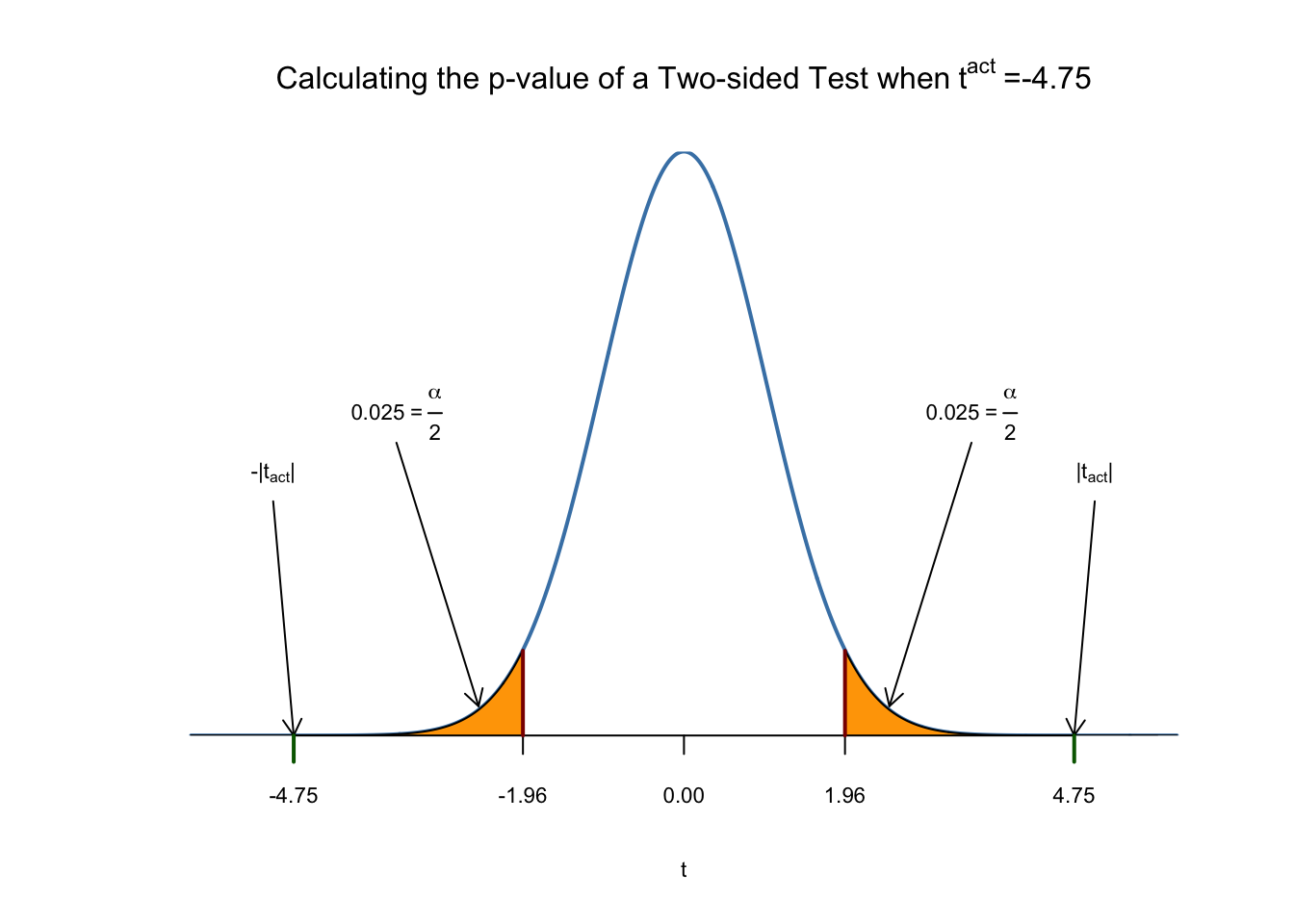
p-Value為曲線左邊的曲線下面積加上曲線右邊的曲線下面積。

---

5.2 回歸係數的信賴區間

信賴水準是信賴區間包含母體參數真實值的信心或信賴度。

信賴水準以1- α 表示，其中 α 為允許錯誤的機率。

例如 95%的信賴水準是指在此信賴水準之下，所建立的信賴區間有 95% 的機率(可信度、信心)會包含母體參數的真實值。

使用 for() 迴圈從 $N(5,25)$分佈中抽樣 $100$ 個觀察值，並在迴圈的每次迭代中計算 ${\mu }^{}$ 以及置信區間的邊界。

mean(CIs[, 1] <= 5 & 5 <= CIs[, 2])

覆蓋 $\mu =5$ 的區間比例為0.9487，無法拒絕$H_0:\mu =\mathrm{5的假設}$

(95%的信賴水準意義：重複建立100個區間，約有100 * 95 % =95個區間包含母體/約有100 * 5% = 5個區間不會包含母體)