4.1 簡單線性迴歸
# Create sample data
STR <- c(15, 17, 19, 20, 22, 23.5, 25)
TestScore <- c(680, 640, 670, 660, 630, 660, 635)
# Print out sample data
STR
#> [1] 15.0 17.0 19.0 20.0 22.0 23.5 25.0
TestScore
#> [1] 680 640 670 660 630 660 635
# create a scatterplot of the data
plot(TestScore ~ STR,ylab=”Test Score”,pch=20)
# add the systematic relationship to the plot
abline(a = 713, b = -3)
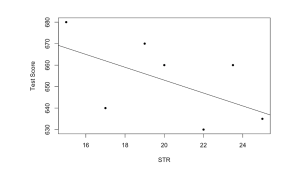
迴歸式為:
4.2估計線性迴歸模型的係數
觀察師生比與考試成績的散佈圖,點的分布非常分散且呈現負向相關,由此結果可以得知師生比越大的班級分數越低。
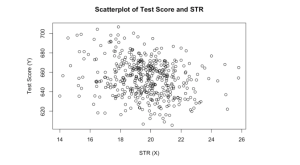
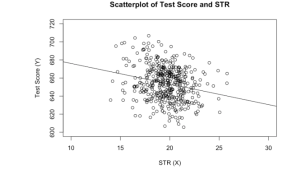
4.3 適合度檢定
這個章節介紹幾個用來用於評估模型的解釋能力和預測能力的迴歸分析概念
1.ESS (Explained Sum of Squares) – 解釋變異和: ESS 衡量了模型中自變量解釋的變異程度。它是因變數的變異減去回歸模型的殘差變異的總和,表示由模型解釋的變異。
2.TSS (Total Sum of Squares) – 總變異和: TSS 衡量了因變數的總變異程度,即觀測值與因變數平均值的差異的總和。
3.RSS (Residual Sum of Squares) – 殘差變異和:RSS 衡量了模型無法解釋的變異,即觀測值與模型預測值之間的殘差的平方和。
公式:TSS=ESS+RSS
在回歸分析中,也經常使用R平方(Coefficient of Determination)來衡量模型的解釋能力。
4.4最小平方法的假設
假設 1:誤差項的條件平均值為零
會使用到R語言的幾個語法:
- runif() – 產生均勻分佈的隨機數
- rnorm() – 產生常態分佈的隨機數
- Predict() – 根據lm()等模型擬合函數的結果進行預測
- lines() – 將線段加入現有繪圖中
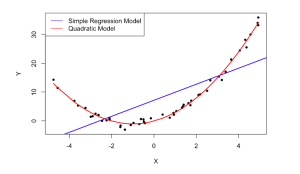
假設2:獨立同分佈的數據
我們隨著時間的推移對同一單位進行觀察。例如,採取X隨著時間的推移,生產公司的工人數量,由於產業轉型,公司會定期裁員,但也存在與經濟、政治等相關的不確定因素影響。
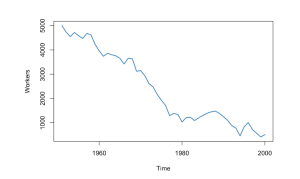
明顯的在這個例子中,對僱員數量的觀察不能是獨立的:今天的就業水準與明天的就業水準。因此,獨立同分佈假設被違反。
假設 3:不太可能出現大的異常值
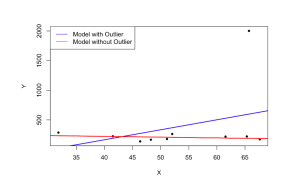
觀察結果過度偏離資料的正常範圍,這樣的結果被稱為異常值。極端值在回歸係數未知的情況下會有很大一部分的比例影響迴歸分析的結果,導致回歸估計的結果失真,建議在估計模型之前排除它們,因為 OLS 對異常值很敏感。
4.5 OLS的採樣分佈
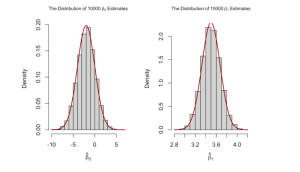
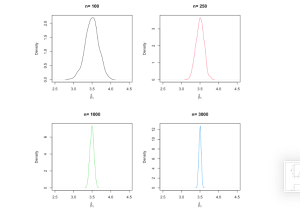 隨著的分佈集中在其平均值附近,即其變異數減少。我們增加樣本量,觀察到接近的分佈,可以觀察到相同的行為。
隨著的分佈集中在其平均值附近,即其變異數減少。我們增加樣本量,觀察到接近的分佈,可以觀察到相同的行為。
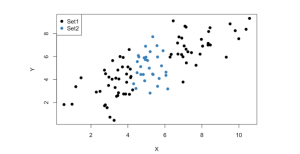
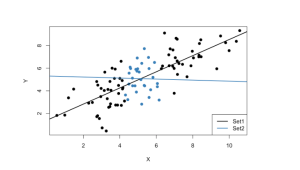
接近樣本平均值的觀測值比那些較遠的觀測值具有較小的變異數。現在,如果我們要透過這兩個集合中的任何一個盡可能準確地畫一條線,很直觀的是,選擇黑點指示的觀測值,即使用方差比藍色觀測值更大的觀測值集,結果會是這樣。以更精確的方式。