此次挑選了3023信邦、2884玉山金、1414東和以及2454聯發科等四支國內上市股票,其分別是電子零組件大廠、金融控股公司、傳產紡織業和全球領先的半導體IC設計公司。研究區間從2021/02/02至2023/03/01,共501個交易日的日收盤價,計算出其日報酬率。
| rate of return | 信邦
0.05091% |
玉山金
0.01274% |
東和
0.10001% |
聯發科
0.00063% |
| SD | 2.22949% | 1.18105% | 2.63591% | 2.57338% |
以上是四支股票所計算出的平均報酬率和標準差(風險),可以看到東和有最大的平均報酬,但其風險值亦大,而聯發科的報酬最小卻也有較大的風險,信邦在這之中的則有較平衡的報酬率-標準差;玉山金就如許多存股族的保守選股標的,有最小的波動(風險),但其報酬亦偏小。
以下是四支股票的共變異數矩陣和其相關係數:
| Cov | 信邦 | 玉山金 | 東和 | 聯發科 |
| 信邦 | 0.000497063 | |||
| 玉山金 | 5.36411E-05 | 0.000139488 | ||
| 東和 | 0.000114776 | 4.74834E-05 | 0.000694804 | |
| 聯發科 | 0.000166199 | 8.23828E-05 | 9.50466E-05 | 0.000662229 |
| Correlation | 信邦 | 玉山金 | 東和 | 聯發科 |
| 信邦 | 1 | |||
| 玉山金 | 0.203715448 | 1 | ||
| 東和 | 0.195306033 | 0.152525647 | 1 | |
| 聯發科 | 0.289679386 | 0.271059303 | 0.140120379 | 1 |
| 報酬 | |||||
| MIN | 0 | 0 | 0 | 1 | 0.000627% |
| MAX | 0 | 0 | 1 | 0 | 0.100005% |
| 0 | 1 | 0 | 0 | 0.012738% | |
| 1 | 0 | 0 | 0 | 0.050912% |
為計算出此投資組合的最大/最小報酬,我分別以全部持股權重都持有其中單一股票,得出最大報酬是全部持有東和;最小報酬則是全部持有聯發科。
下圖以最大/最小報酬,中間切分,共20個報酬率,再以規劃求解找出在此20個報酬率下,最小風險的個別權重。而此權重的限制為0到1之間,意即只能選擇不持股或買進持股,而無法做空
| 投資組合的風險 | 投資組合的報酬率 | 信邦 | 玉山金 | 東和 | 聯發科 | |
| 1 | 0.026359127 | 0.1000052% | 0 | 0 | 1 | 0 |
| 2 | 0.024127448 | 0.000947747 | 0.106541965 | 0 | 0.893459035 | 0 |
| 3 | 0.02226088 | 0.000898196 | 0.207472518 | 0 | 0.792527482 | 0 |
| 4 | 0.02077502 | 0.000851252 | 0.303094683 | 0 | 0.696905319 | 0 |
| 5 | 0.019626723 | 0.00080678 | 0.331911368 | 0.034749403 | 0.633339229 | 0 |
| 6 | 0.018589469 | 0.000764648 | 0.316596699 | 0.091644555 | 0.591758744 | 0 |
| 7 | 0.017634109 | 0.000724733 | 0.302088083 | 0.145545217 | 0.552366699 | 0 |
| 8 | 0.016757734 | 0.000686919 | 0.288343044 | 0.196609023 | 0.515047934 | 0 |
| 9 | 0.015957496 | 0.000651095 | 0.275321487 | 0.244985224 | 0.47969329 | 0 |
| 10 | 0.015230568 | 0.000617157 | 0.262985214 | 0.290815344 | 0.446199442 | 0 |
| 11 | 0.014574092 | 0.000585005 | 0.251298251 | 0.334233332 | 0.414468415 | 0 |
| 12 | 0.01398514 | 0.000554546 | 0.240226386 | 0.375366168 | 0.384407444 | 0 |
| 13 | 0.013460673 | 0.000525689 | 0.229737231 | 0.414334131 | 0.355928637 | 0 |
| 14 | 0.012997504 | 0.000498351 | 0.219799982 | 0.451251837 | 0.328948181 | 0 |
| 15 | 0.012592326 | 0.047245213% | 0.2103861 | 0.486225133 | 0.303388767 | 0 |
| 16 | 0.012241623 | 0.044791623% | 0.201467494 | 0.519358408 | 0.279174098 | 0 |
| 17 | 0.011941763 | 0.042467169% | 0.193018146 | 0.550748419 | 0.256233435 | 0 |
| 18 | 0.011689012 | 0.040265055% | 0.185013808 | 0.580485153 | 0.234501039 | 0 |
| 19 | 0.01147953 | 0.03817884% | 0.177430586 | 0.608657372 | 0.213912041 | 0 |
| 20 | 0.025733807 | 0.0006270% | 0 | 0 | 0 | 1 |
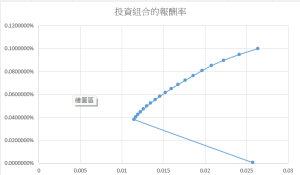
上圖投資機會集合軌跡,即是以上面20個點所得出,橫軸(X軸)為風險,縱軸(Y軸)為報酬率。
在固定相同的報酬率下,找到最小的風險,因此在藍色軌跡IOS的右側和下半部是被支配的(非最佳),而軌跡左側則是無法達到(不可及)的。
在所有組合中,有最小風險的位置會在此圓弧軌跡的左端點,此點又稱為最小變異投組-MVP,以此點為起點往上才是有效率最佳的投資組合,即效率前緣。
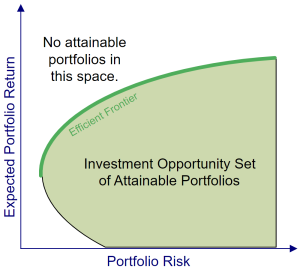
資料來源: https://thismatter.com/money/investments/modern-portfolio-theory.htm
上圖即為理論操作,在Efficient Frontier上是所有的最佳投資組合,而在此效率前緣上,擁有最高夏普比率Sharpe ratio的最佳投組,稱為市場投資組合(market portfolio)。
